焦点弦长公式。
给大家讲了一下这三种曲线的焦半径之间统一的关系。这里就是这样一个情况,它们有一个统一的形式,都是ep分之2。因为抛物线零距离是e,所以这里就可以写成是p分之2。需要注意的是这个地方得交于意志,这样才可以。就是在交于意志会有这个结,交于两支是不行的。
今天要给大家讲的是什么?叫焦点弦,不是焦半径,就是焦点弦整个的长度。它们其实也会有一些性质,先写出来。
·比如像抛物线当中都是讲的是焦点在f轴上的,在y轴上可能会变。ab是2p除以3c大方,2p就是y方等于2p。2p大是什么?c大是焦点弦的倾斜角。
·椭圆当中焦点弦ab是等于几的?它就稍微复杂一点,这是2p去除以一个一减去一个一方乘以cosinc的方,待会给大家去证明推导。
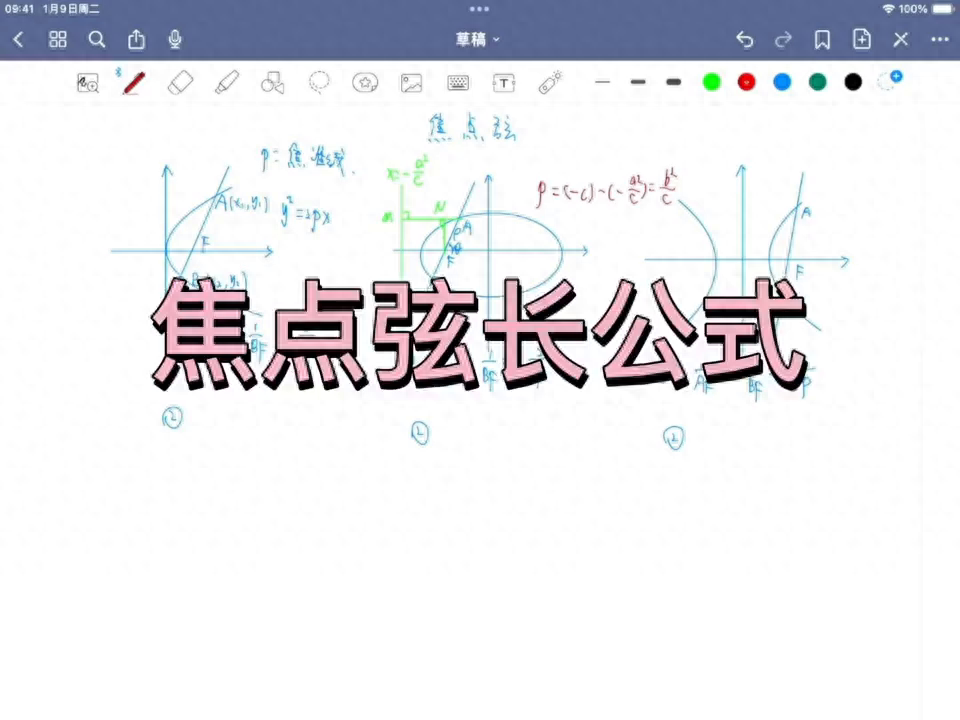
·再看一下双曲线,双曲线注意也同学说是一样的,其实上来讲它跟椭圆还是有点不一样的。因为看一下这个问题,就是分母有可能会是什么情况会小于0,因为一方是大于一的,这里是0到1的,乘完之后可能会大于一。
所以怎么办?其实上来讲需要给它加一个绝对值。加绝对值的原因是什么?其实就是这个地方适用于教育一只是可以的,教育两只也是适用的,就是要加一个绝对值,然后保证一下正的就行了。
现在给大家去证明一下,证明一下的方式也有多种,比如像第一个,这个。
·这个AB大概先写一写,就是法一,像AB是等于AF加上一个BF的,其中BF就是S1加2分之匹,然后BF就是X2加2分之匹,转换成到准线的距离,所以它就写成S1加X2再加上一个P,然后连一下就可以了。
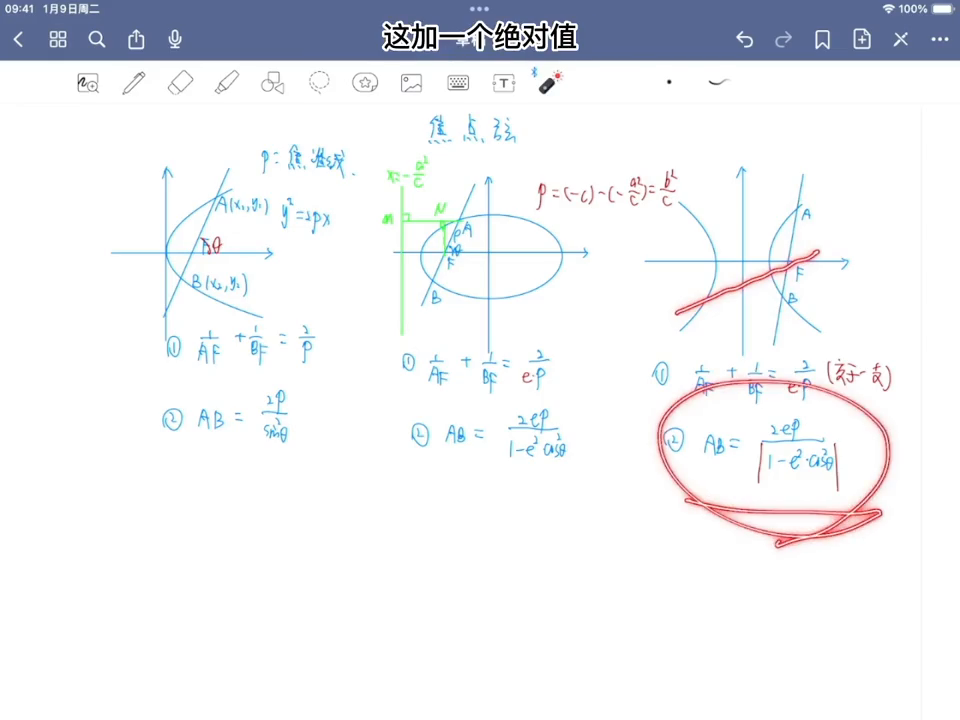
·这个直线是XY写成了是x等于MY加上一个2分之P,刚才觉得结局是2分之P,然后跟官方等于2PS进行连立,连立的时候显然是削这个谁?削X比较方便,所以削掉,得到这样一个情况。
·在这样一个情况下继续往下写,是Y方减去2PMY再减去P方等于0,可以把Y1加Y2写出来就是2PM,这时候再去写X加X2,因为想要的是X加X2,S1加X2对,用这个东西,X1是等于MB的Y1加2分之P的,然后X2是等于MB的Y2加2分之P,所以这个结果就是M倍的Y1加Y2再加上一个P。
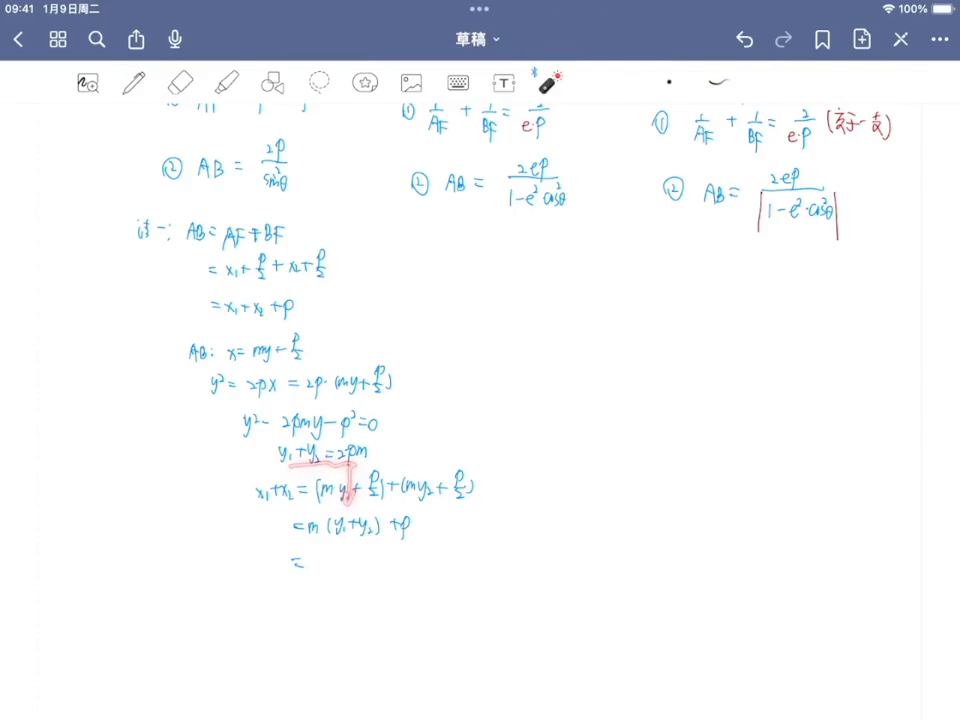
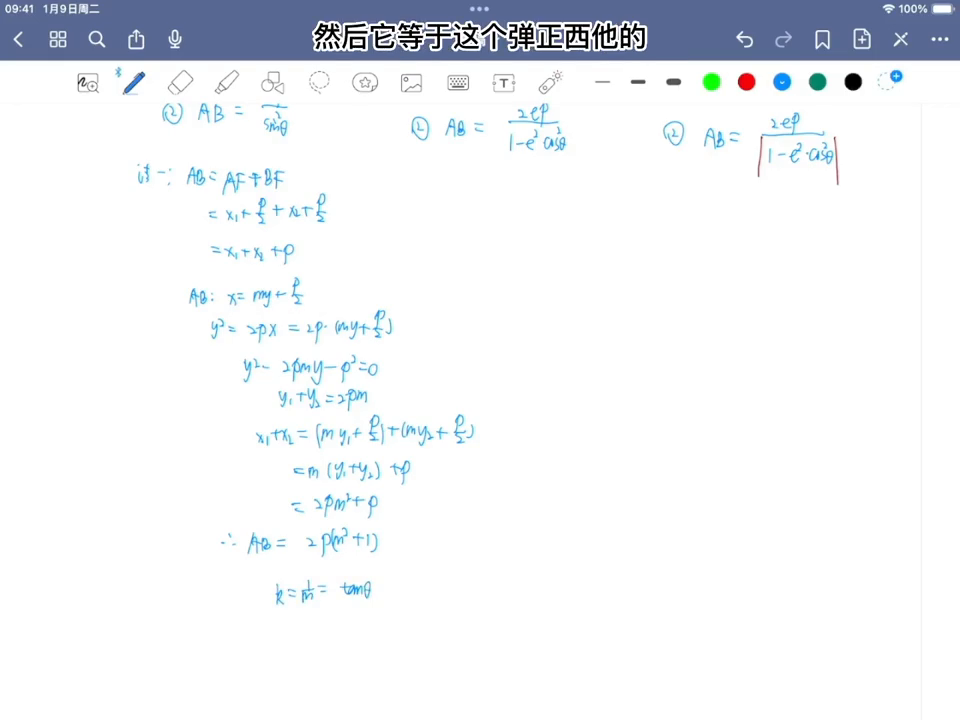
·所以把两根之和Y1加Y2带进来,发现它就是2PM方再加个P,所以弦长AB等于什么?等于相当于是S加X再加了个P,就是2PM方再加个2P,提一个2P出来,就这个结果。
·接下来需要看一下最终结果是关于倾斜角的情况,m跟倾斜角有什么关系?m看一下直线这样设的,所以这样子的,就是m分之一的,然后它等于弹正西,所以可以得到m方再加一等于弹正西方分之一再加一,弹正西方是等于什么?等于括三方除以三方的,再加个一,所以要通分一下,上面就是co三方加三方分子就是一了,然后分母上就是三方。
所以整个式子来讲是不是就可以得到了ab的长度就是2p乘以方,三方分之一也就是2p除以三系的方,只有这个,这是第一种方法证明。
再用第二种方法去证明一下,第二方法其实比这个简单一点,第二方法是偏几何的方法,刚才是偏带数的方法,给大家去画一个图,把准线画出来,这里也这样,这里是a,这里是b,这个是f,这个地方假设是m,这个地方是n的画,可以看一下af的长,这里是c,af的长可以这样去写,是af是等于几?等于am,而其中am等于几?am等于这个,就等于这个地方是e,它等于ae加上一个em,而ae等于几?等于am复去乘以扩散,其他对不对?
这是set,em就是p,交准句对不对?所以大家看一下,项就是一减call三set乘以af等于p,所以af是什么?就是p除一减call三set,同理大家去看一下,再去写BF,BF一样的用这种方式对吧?只不过在写bn的时候它的想法是什么?是这段p减去这一段,就刚才这个地方应该是一个减,p减去那一段,所以这个bf是等于什么?等于这个p去除以这个一加上一个cos3系的。
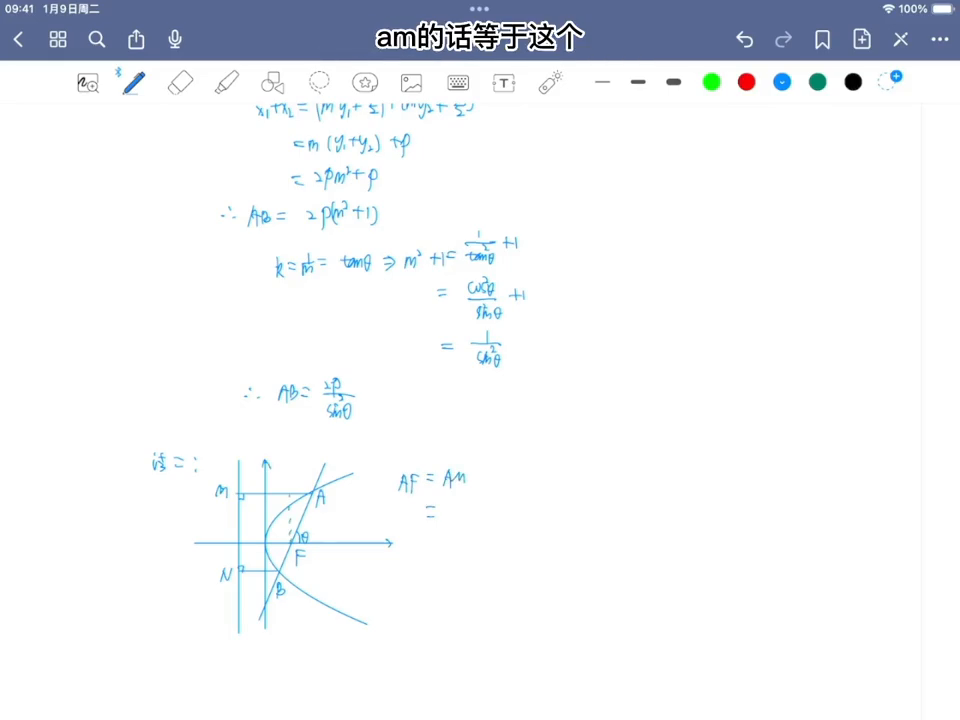
所以大家去看一下这个af加上一个bf也是我们的这个交点弦长,等于它俩通分一下,就是p倍的,一减扣三系它方,通分完上面是2p,然后一减扣三系它方就是这个cos3方,所以就得到了。
这是这个情况,这种方法其实就是什么?就是上次的视频给大家去讲第二定义,在椭圆和双曲线当中很像,但是正椭圆双曲线用的就是这种方法,它显得会简单一些,是吧几何法。
看一下后面的这个第,这两个只证明一个,它俩就差不多的,还是以椭圆为例来去证明,用的方法跟证明第一个性质的方式是一样的。还是这两段,先这个算出来,比如说像af,再算一遍,af等于谁?等于一倍的am,这是第二定义。
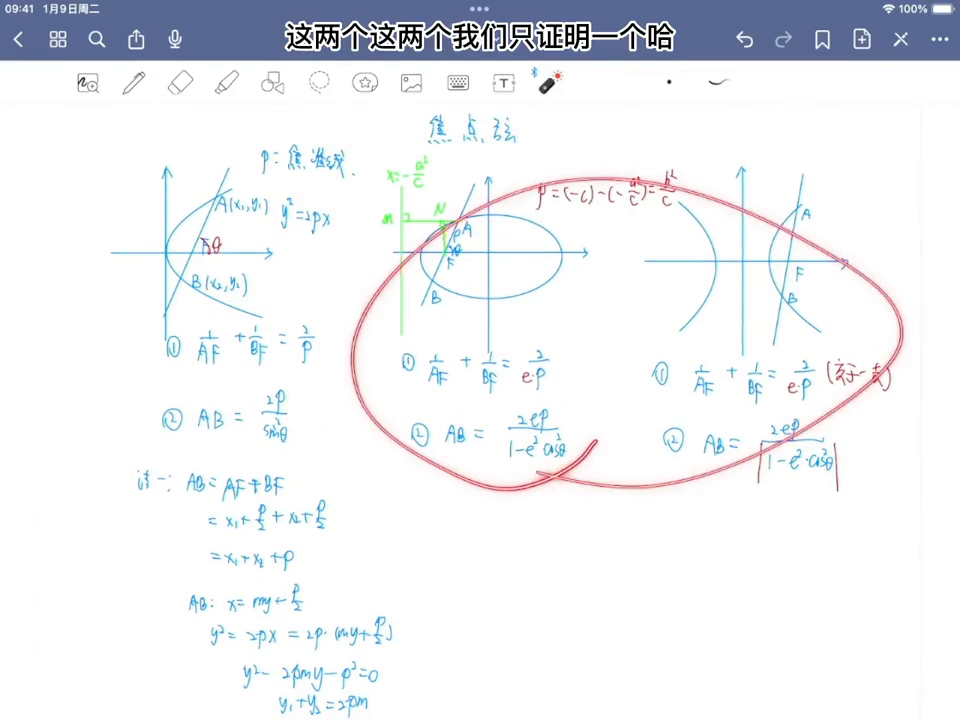
第二定义到焦点距离比上到准线的距离等于离心率,其实这个am可以写成谁?可以写成是mn,再加上一个mn,然后mn写一写,mn这个地方其实就是这段af乘以cosinct对不对?所以就是af乘以cosinct,再加上一个mm,其实就叫p。
注意这个p是什么p?叫这个标准句,就这个,这个之前算过了,也是用p来表示,然后这样去掉括号,再移下项,移到左边距是一减去一倍的call3系,它乘以这个af,这个结果就是ep,所以大家看AF就是EP去除以一减去一倍的靠3系统,同理再去写BF,一样的道理,这个地方再弄一个出来,比方这个地方再做一个垂直出来,BG这些的,还是利用刚才类似的方式去算一下,可以算出来是BF的值,EP是除以弦除以e加上一个e倍的COS3系统。
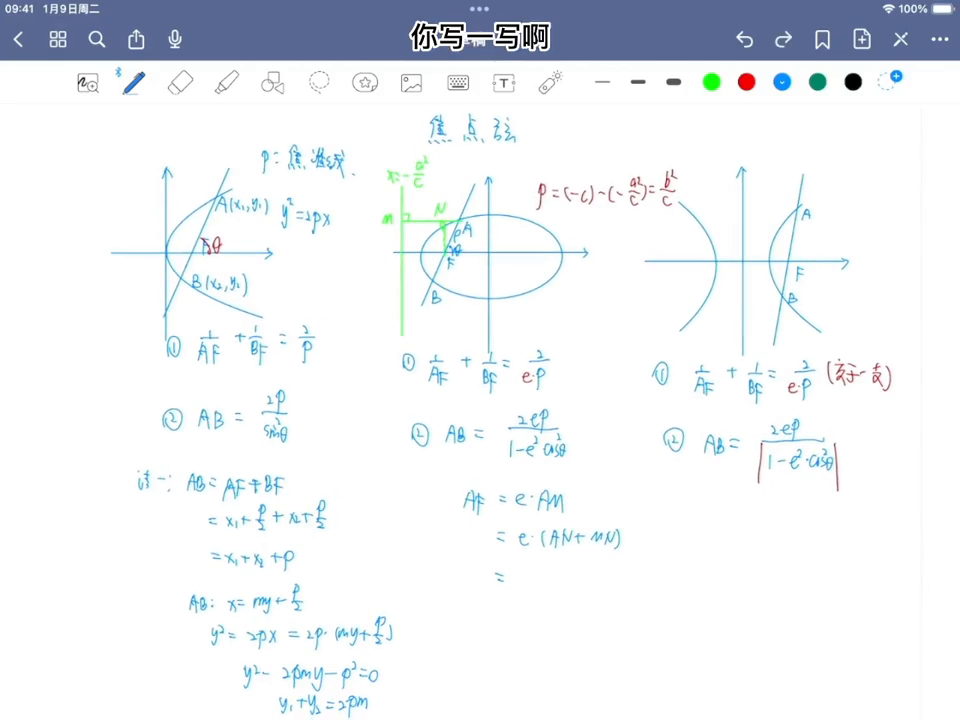
所以大家去看一下焦点弦就等于它俩相加,它俩相加得给它通分一下,这个地方通分一下,通分一下它的分子是一样的,分母有个平方差的公式,就写出来是一减去一方乘以call3,其他方上面是二倍的一批了,就这个结果,这也就是刚才写的结论,就证明出来了。
双曲线当中类似的方式,但是要加个绝对值,刚才给大家解释过原因了。关于这个再给最后给大家去说一下,就是觉得什么东西这么难记,还好一点点,抛物线好一点点,怎么记可以不记,这个地方只是给大家说一下有这么回事,你知道还是有这么回事,这就行了。
对于这个自己去选择,有些题如果知道确实会好做一点点,但是要记住,记住的方式是什么?只能写到整理上去,反复的去观看它了,反复的复习了,就这样一个方式。
