不知道您是否和老黄原来想的一样,以为泰勒公式只能在x0附近逼近原函数。比如当x0=0时的泰勒公式(即麦克劳林公式),就只能在原点附近逼近原函数。看完这个例题,您就会和老黄一样豁然开朗,明白泰勒公式逼近原函数的实质的。
用麦克劳林多项式逼近正弦函数sinx,要求误差不超过10^(-3).试以m=1,m=2两种情形分别讨论x的取值范围.
分析:如果按老黄原来的想法,那么x的取值范围肯定是很小的,就是只能在原点的附近。我们来解一解这个问题,看看是不是这样的。
首先,写出sinx的带有拉格朗日余项的麦克劳林公式:
sin=x-x^3/3!+x^5/5!+…+(-1)^(m-1)x^(2m-1)/(2m-1)!+(-1)^mcos(θx)x^(2m+1)/(2m+1)!, x∈R.
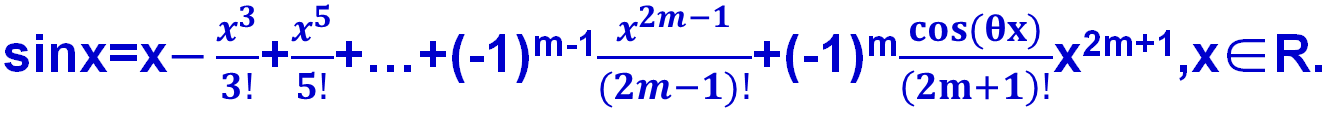
这是泰勒公式在x0=0的定量形式,只有定量形式,才能保证误差在要求的范围内。带有佩亚诺余项的麦克劳林公式是定性公式,没有这个功能。
所谓误差不超过10^(-3),指的是泰勒公式(这里是麦克劳林公式)中的拉格朗日余项不大于10^(-3), 即(-1)^mcos(θx)/(2m+1)!≤10^(-3).
解:(1)当m=1时, sinx≈x,
要使误差满足|R2(x)|=|-x^3cos(θx)|≤|x^3|/6≤10^(-3),
只须使|x^3|≤6×10^(-3),即|x|≤0.1817,【注意,这里取近似值,都要采用退一法,而不能采用四舍五入法,更不能采用进一法,否则就有可能造成答案不正确,下同】
大约有-10⁰24’40”≤x≤10⁰24’40”.
(2)当m=2时, sinx≈x-x^3/6,
要使误差满足|R4(x)|=|-x^5cos(θx)|≤|x^5|/120≤10^(-3),
只须使|x^5|≤0.12,即|x|≤0.6543,
大约有-37⁰29’38”≤x≤37⁰29’38”.
可以看到,这两个结果,和老黄原先设想的,还是有比较大的差别的。下面结合图像观察,更能说明问题。
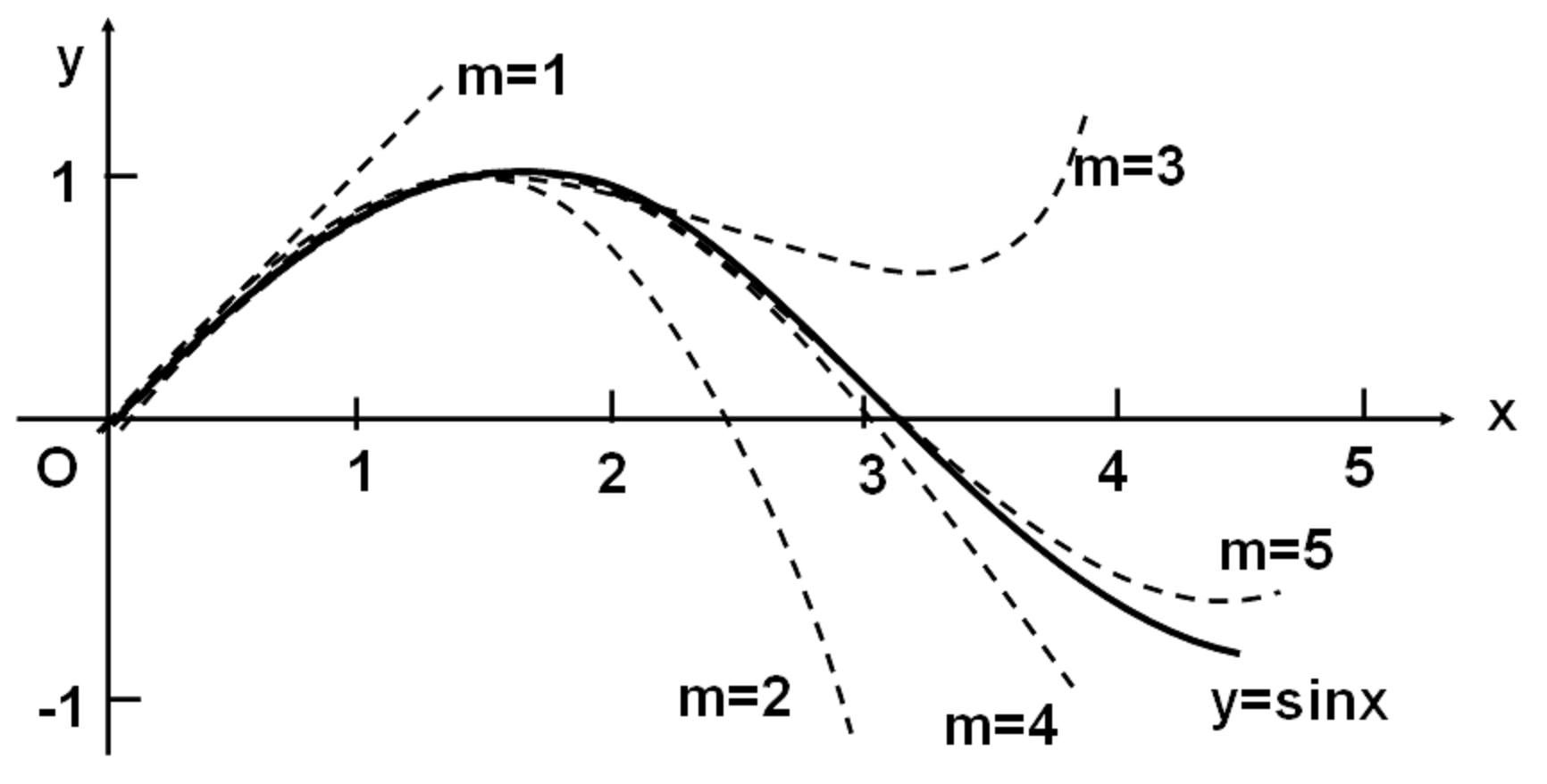
如上图(图画得不甚准确,但足以说明问题),图中实线图像是正弦图像的一部分,虚线图像是m不同取值下的麦克劳林多项式的图像的一部分。可以看到:
当m=1时,麦克劳林多项式是y=x,的确只能在原点附近逼近正弦函数。当m=2时,麦克劳林多项式逼近正弦函数的范围明显大了不少。当m=3时,逼近的范围已经接近正弦函数的一个周期了(还有半个周期在定义域的负区间上)。当m=4时,逼近范围超过了一个周期。当m=5时,逼近范围又更大了。可以推知,当m足够大时,麦克劳林多项式就可以非常逼近整个正弦函数的图像。
因此在x0附近,未必要用在x0的泰勒公式逼近原函数,这样做的好处只是m(或n)不用取得非常大,取m=1就足够了。而用麦克劳林公式在任意点x0逼近原函数,则只需m取得足够大就可以了,x0与原点的距离越大,m的取值就越大。
注意观察,我们至少还可以有两点发现:
1、为什么sinx的泰勒多项式只有奇数次项呢?因为这样的多项式有奇函数的性质,符合正弦奇函数的特性。
2、正弦函数的泰勒多项式的常数项为什么是0呢?因为sinx过原点,所以只有这样的多项式,才能更好地逼近sinx。
现在您能理解泰勒公式的实质了吗?
